Курс: Информационные технологии. Системы счисления. Задачи.

Общее

Свернуть всё Развернуть всё

Выбрать элемент Объявления

Объявления Форум

Тема 1

Выбрать элемент Текст и медиа

Количественный эквивалент некоторого положительного числа A определяется:

A_(p)= a_n-1*p^n-1 + a_n-2*p^n-2 + …+a₁*p¹ + a₀*p⁰ ,

где: p – основание системы счисления (нек. целое пол. число);

a – цифра данной системы счисления;

n – номер старшего разряда числа.

Перевод из двоичной системы счисления в десятичную

A₍₂₎= a_n-1*2^n-1 + a_n-2*2^n-2 + …+a₁*2¹ + a₀*2⁰

1110010₍₂₎

1*2⁶+1*2⁵+1*2⁴+0*2³+0*2²+1*2¹+0*2⁰=64+32+16+0+0+2+0=114₍₁₀₎

Из десятичной системы счисления в двоичную

11110111

Из шестнадцатеричной системы счисления в десятичную

Десятичн. число	Двоичное число	Шестнадцатер. число
0	0000	0
1	0001	1
2	0010	2
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	0111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F
16	10000	10

3C₍₁₆₎

3*16¹+12*16⁰=3*16+12*1=48+12=60

Перевод из десятичной системы счисления в шестнадцатеричную

7FFF

Из шестнадцатеричной системы счисления в двоичную

E4D5₍₁₆₎=1110 0100 1101 0101 ₍₂₎

Перевод из двоичной системы счисления в шеснадцатеричную

1110 0101 1010 1111 0101 1000 1101 1000 ₍₂₎ = E5AF58D8

Выбрать элемент Конспект к теме 1

Конспект к теме 1 Файл DOCX
Выбрать элемент Тест 1 к теме 1 (количество попыток: 2)

Тест 1 к теме 1 (количество попыток: 2)

Открыто с: среда, 27 марта 2024, 00:05

Закрывается: среда, 27 марта 2030, 00:05
Выбрать элемент Тест 2 к теме 1 (количество попыток: 2)

Тест 2 к теме 1 (количество попыток: 2)

Тема 2

Выбрать элемент Текст и медиа
Выбрать элемент Система счисления позволяет по определенным правил...

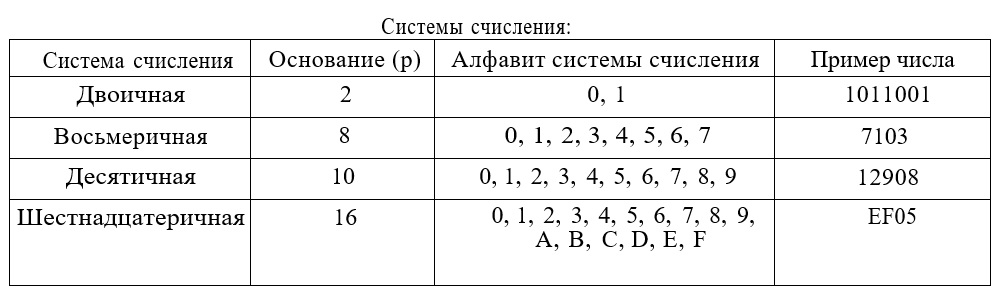
Система счисления позволяет по определенным правилам записать числа при помощи символов какого-либо алфавита (цифр, знаков).

Системы счисления бывают позиционные и непозиционные.

В позиционных количественные значения цифр зависят от их позиций (разрядов) в числе.

В непозиционных значение числа получается путём суммирования, вычитания количественных значений цифр, не зависящих от их местоположения в числе. Римская система счисления – непозиционная.

Числа могут записываться в виде суммы произведений его цифр на основание системы счисления в степени, равной значению разряда той или иной цифры числа (для целого числа нумерация разрядов ведётся с нуля справа налево, для дробного числа нумерация разрядов ведётся от десятичной запятой влево по возрастанию, а вправо - по убыванию, при атом разряду единиц присваивается нулевой номер).

Перевод двоичного числа в восьмеричную cucтeму счисления производится по триадам:

Перевод двоичного числа в шестнадцатеричную систему счисления производится по тетрадам:

Правила выполнения арифметических действий над двоичными числами

При сложении двоичных чисел в каждом разряде производится сложение разрядов.

Примеры решения задач

Задача 1. Как представлено число 87₁₀ в двоичной системе счисления?

1) 1010111₂              2) 1010101₂               3) 1010011₂              4) 1000100₂

Решение

Достаточно выполнить перевод заданного числа в двоичную систему счисления путём

последовательных делений «в столбик» на 2:

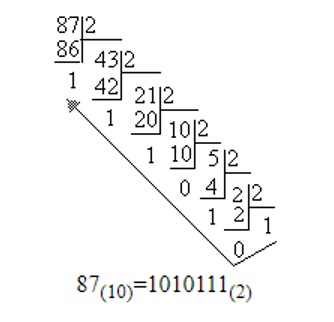
Ответ: 78₁₀ = 10101112

Задача 2. Дано А = A7₁₆, В = 251₈. Какое из чисел С, записанных в двоичной системе,

отвечает условию А < С < В ?

                                          1) 101011002       2) 101010102        3)101010112       4) 101010002

Решение

Восьмеричное и шестнадцатеричное число переводится в двоичную систему счисления по триадам и тетрадам:

A = A7₁₆ = (A₁₆=1010₂) (7₁₆=0111₂) = 10100111₂

B = 251₈ = (2₈=010₂) (5₈=101₂) (1₈=001₂) = 010101101₂

                   Записываются полученные двоичные значения в заданный «шаблон» неравенства:

101001112  <          < 1010100123

Ответ: С = 10101000₂.

3aдача 3. Вычислите значение суммы 10₂ + 108 + l0_16i в двоичной системе счисления. 1) 10100010                    2) 11110               3) 11010 4) 10100

Решение

Перевести все числа в десятичную систему счисления, выполнить вычисления в ней, а затем выполнить перевод результата из десятичной системы счисления в требуемую:

10₂ = 2;

108 = 8;

10₁₆ = 16;

2 + 8 + 16 = 26;

                    26₁₀= 11010₂

Ответ: 11010₂.
Выбрать элемент Конспект к теме 2

Конспект к теме 2 Файл DOCX
Выбрать элемент Тест к теме 2 (количество попыток: 2)

Тест к теме 2 (количество попыток: 2)

Открыто с: вторник, 21 ноября 2023, 23:28

Закрывается: суббота, 21 ноября 2026, 23:28

Тема 3

Выбрать элемент Текст и медиа
Выбрать элемент Задача 1. В системе счисления с некоторым основани...

Задача 1. В системе счисления с некоторым основанием число 12 записывается в виде 110. Укажите это основание.

Решение

Развёрнутая форма записи числа в системе счисления с основанием n при его переводе в десятичную систему:

d₁₀ = a_m* n ^m+ … + a₂* n² + a₁* n¹+ a₀

неизвестное основание системы счисления обозначается - n

12 = 1*n² + 1* n+ 0

n² + n- 12 = 0

дискриминант

D = b²-4*a*c = 1 + 4*12 = 49

n₁ = (-b - Öd)/(2*a) = (-1 – 7)/2 = - 4 n₂ = (-b + Öd)/(2*a) = (-1 + 7)/2 = 3

Ответ: 3 – троичная система счисления

Задача 2. В системе счисления с некоторым основанием десятичное число 49 записывается в виде 100. Определите это основание.

Решение

49 = 1*n² + 0 * n+ 0

n² = 49

n₁= - 7

n₂= 7

Ответ: 7 – семиричная система счисления

Задача 3. В системе счисления с некоторым основанием десятичное число 27 оаписывается в виде 30. Определите это основание.

Решение

27 = 3 * n + 0

3 * n = 27

n = 9

Ответ: 9 – девятеричная система счисления
Выбрать элемент Конспект к теме 3

Конспект к теме 3 Файл DOCX
Выбрать элемент Тест к теме 3 (количество попыток: 2)

Тест к теме 3 (количество попыток: 2)

Открыто с: пятница, 1 марта 2024, 23:28

Закрывается: вторник, 3 марта 2026, 23:22

Тема 4

Выбрать элемент Текст и медиа
Выбрать элемент Кодирование. Часть 1. Система счисления — знаковая...

Кодирование. Часть 1.

Система счисления — знаковая система, позволяющая по определённым правилам записывать числа при помощи символов некоторого алфавита.

Такими символами могут быть любые знаки. Во многих задачах можно найти аналогию с той или иной позиционной системой счисления и решить задачу.

Задача 1. Все 5-буквенные слова, составленные из букв Т, О, Н, записаны в алфавитном порядке. Начало списка:

1. TTTTT

2. TTTTO

3. ТТТТН

4. TTTOT

Сколько букв Т встречается в слове, стоящем на 101-м месте от начала списка?

Решение. Букву Т можно заменить на цифру 0, буква О - на цифру 1, букву Н - на цифру 2. Задача преобразуется: Все 5-значные числа, составлены из цифр 0, 1, 2, записаны в порядке возрастания. Начало списка:

1. 00000

2. 00001

3. 00002

4. 00010

Сколько нулей встречается в числе, стоящее на 101-м месте от начала списка?

Числа записаны в троичной системе счисления, с шагом увеличения на единицу. При записи в десятичной системе счисления эта последовательность чисел эквивалентна ряду целых чисел 0, 1, 2, ...

Чтобы определить число, стоящее в списке на 101-й позиции, нужно учесть рассогласование между значениями чисел и их порядковыми номерами в списке:

• последовательность чисел начинается с нуля;

• нумерация чисел в списке начинается с единицы.

Тогда для определения числа, стоящего в 101-й позиции, нужно составить следующее соответствие:

Порядковый номер

Значение числа

1

0

101

(101-1)

На 101-м месте в списке будет стоять десятичное число 100. Необходимо получить пятиразрядную запись этого числа в троичной системе счисления.

Получается на 101-м месте в списке находится пятиразрядное троичное число 10201.

В записи этого числа два нуля. Запись слова, составленного из букв Т, О, Н (при возврате к исходному условию задачи), будет такой: ОTHTО.

Ответ: 2 буквы Т.
Выбрать элемент Конспект к теме 4

Конспект к теме 4 Файл DOCX
Выбрать элемент Тест к теме 4 (количество попыток: 2)

Тест к теме 4 (количество попыток: 2)

Открыто с: вторник, 29 октября 2024, 07:33

Закрывается: вторник, 30 октября 2035, 07:33

Тема 5

Выбрать элемент Текст и медиа
Выбрать элемент Кодирование. Часть 2. Система счисления — знаковая...

Кодирование. Часть 2.

Система счисления — знаковая система, позволяющая по определённым правилам записывать числа при помощи символов некоторого алфавита.

Такими символами могут быть любые знаки. Во многих задачах можно найти аналогию с той или иной позиционной системой счисления и решить задачу.

Задача 1. Все 5-буквенные слова, составленные из букв Т, О, Н, записаны в алфавитном порядке. Начало списка:

1. TTTTT

2. TTTTO

3. ТТТТН

4. TTTOT

Укажите номер в списке слова, которое первым начинается с буквы Н.

Решение. Поскольку слова являются с букв Т, а в последовательности слов после TTTTT стоят слова TTTTO и ТТТТН, то сопоставление букв цифрам будет следующим: T-0, О-1, Н-2. Задача преобразуется:

Все 5-значпые числа, составленные из цифр 0, 1, 2, записаны в порядке возрастания. Начало списка:

1. 00000

2. 00001

3. 00002

4. 00010

Укажите номер числа в списке, которое первым начинается с цифры 2.

Числа в троичной системе счисления, первым числом, начинающимся с цифры 2, является троичное число 20000. Троичное число 20000 преобразуется в десятичную форму. 0*3⁰+0*3¹+0*3²+0*3³+2 *3⁴ = 162.

Чтобы определить номер позиции в списке для числа 162, следует учесть рассогласование между значениями чисел и их порядковыми номерами в списке:

• последовательность чисел начинается с нуля;

• нумерация чисел в списке начинается с единицы

Порядковый номер

Значение числа

1

0

(162 + 1)

162

Десятичное число 162 стоит в списке на 16З-м месте.

Число 20000₃, значит слово HTTTT (первое, начинающееся с буквы Н), будет стоять в списке в 163-й полиции.

Ответ: искомое слово расположено в позиции №163.
Выбрать элемент Конспект к теме 5

Конспект к теме 5 Файл DOCX
Выбрать элемент Тест к теме 5 (количество попыток: 2)

Тест к теме 5 (количество попыток: 2)

Открыто с: вторник, 29 октября 2024, 07:47

Закрывается: вторник, 30 октября 2035, 07:47
Выбрать элемент Итоговый тест. И Конкурс

Итоговый тест. И Конкурс

Открыто с: четверг, 19 июня 2025, 09:00

Закрыто c: суббота, 19 июля 2025, 09:00

Порядковый номер	Значение числа
1	0
101	(101-1)

Порядковый номер	Значение числа
1	0
(162 + 1)	162